A tour of the traveling salesman
Today we're going to be talking about one of those very famous problems in computer science: the traveling salesman problem.
This is an interesting problem both because of its history, the long-storied attempts to solve it, and how it's an example of the kind of tradeoffs you have to consider in the world of "hard problems". We'll make the idea of a "hard problem" more rigorous shortly.
The informal statement of the problem is pretty easy to describe: given a list of destinations and distances between them, calculate the shortest route that goes to each destination exactly once before returning to the start. Such routes are generally called "tours". Let's note a couple of things about the definition of this problem. First off, that we're assuming symmetry in our "roads". No one-way streets. Second, we're assuming that every destination is connected to every other destination simply, so you won't ever have to pass through other locations first. You can always go from A to C directly, you don't have to pass through B first. If you've seen graphs before, it means every instance of a traveling salesman problem can be represented as a fully-connected graph.
Here's an example with five locations and list of distances
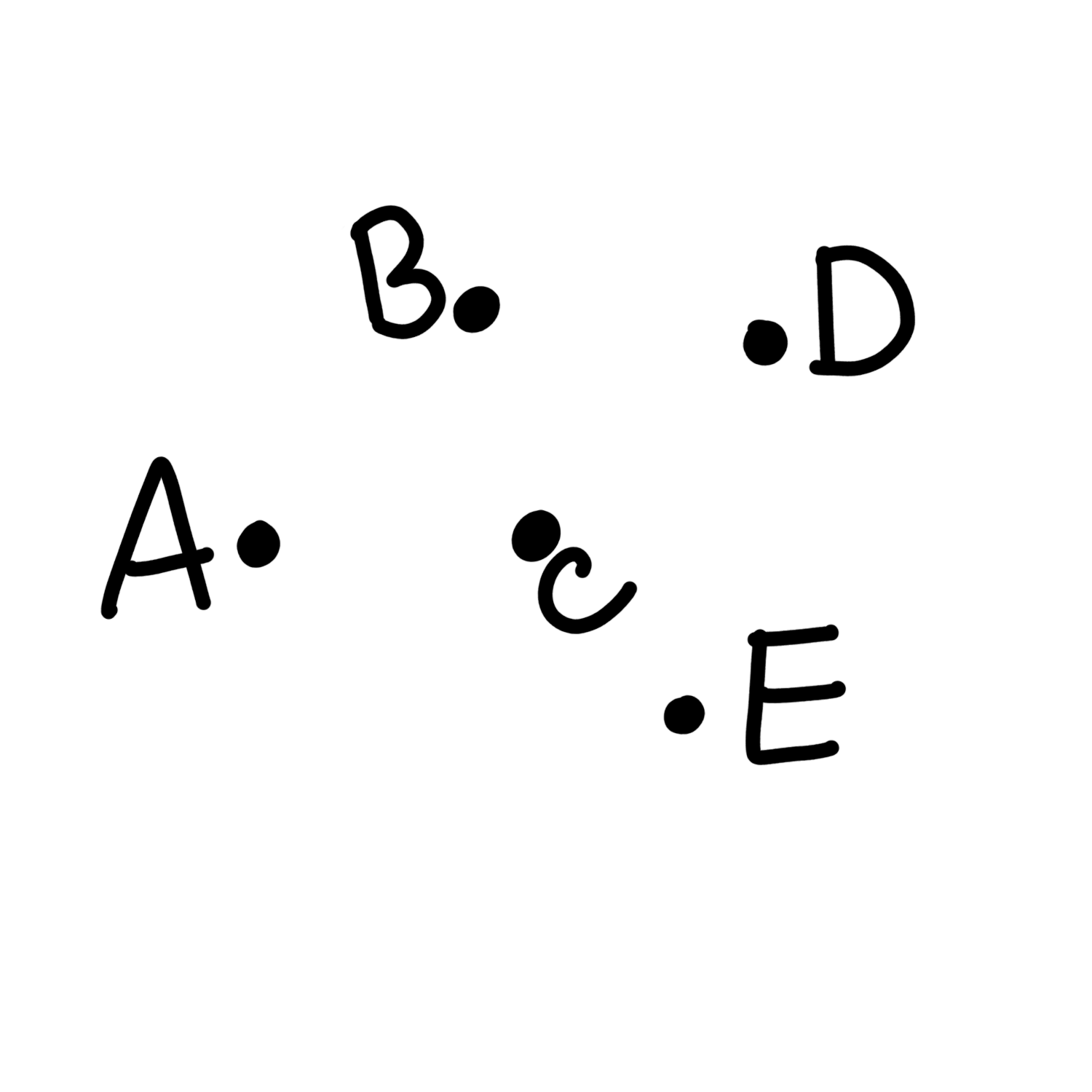
- A -> B: 10
- A -> C: 9
- A -> D: 20
- A -> E: 15
- B -> C: 8
- B -> D: 14
- B -> E: 25
- C -> D: 9
- C -> E: 11
- D -> E: 20
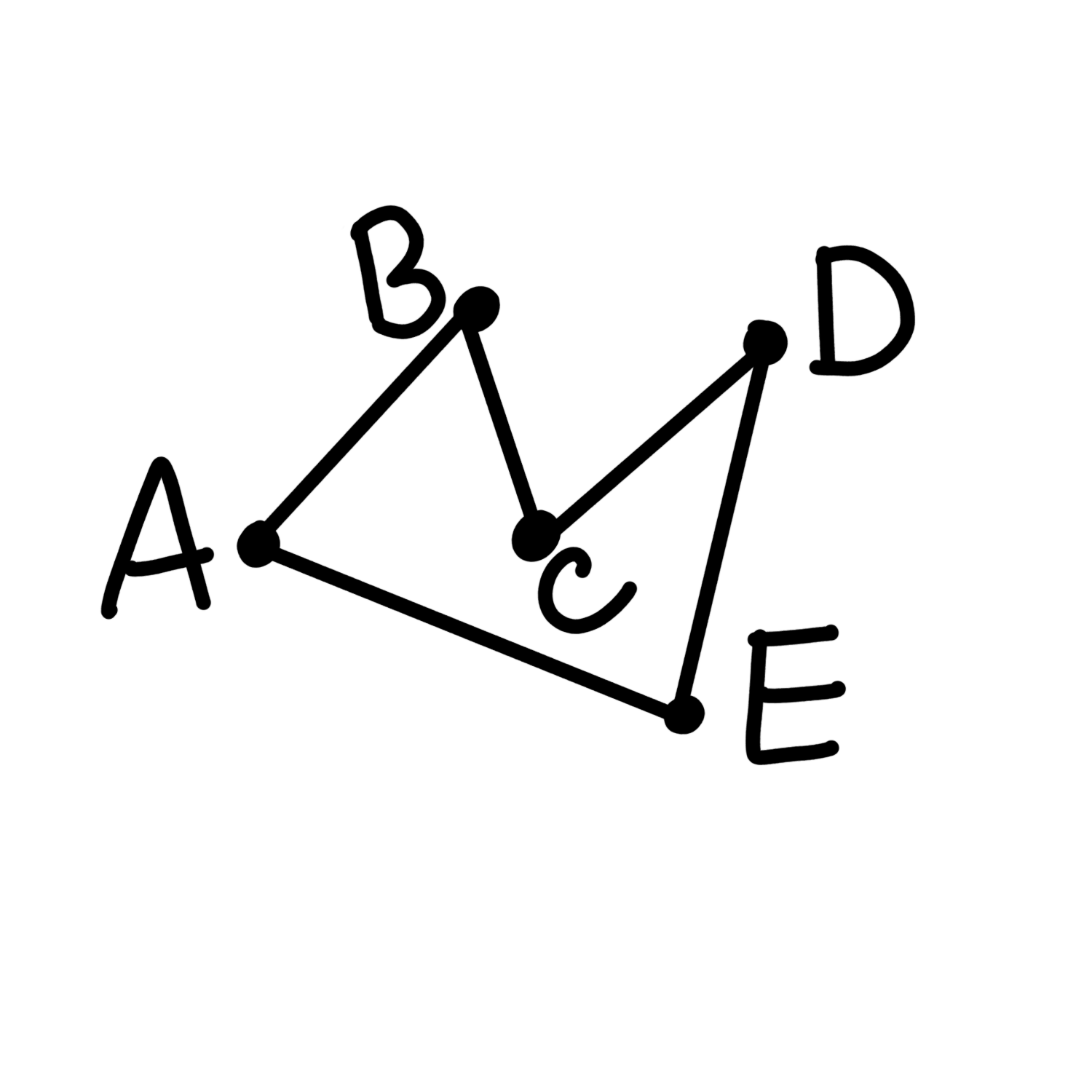
This leads to an optimal solution that looks like this, with a length of 62
Okay so part of what's interesting here is that while this problem comes from the very literal question of "how do you plan the most efficient route between a bunch of cities", it kinda shows up all over the place, really any time you have something that kinda be represented as a 2-d layout with distances you're probably not far from it being a kind of traveling salesman problem. It shows up in manufacturing a lot: choosing the right order for drilling into a circuit board or putting solder on leads, the movement of a laser when etching onto a chip, optimizing the movement of cnc mills like you might see in a makerspace, or even additive 3d printing where you have a nozzle that is going to raise and lower to put plastic fillament in places. A really kinda fun example to me involves the movement of a telescope to observe a set of objects. You really want to move it as little as possible because it's a slow process of delicate machinery, so it's important to optimize how much you're moving it so you're not swinging the apparatus anymore than you have to.
Taking a step back, maybe this doesn't sound like it should be a hard problem. I know to me, on some level, it doesn't feel like it should be. Which I think is interesting because it's been shown that people are often pretty good at coming up with reasonably good solutions—though not the best solution—to problems like these very quickly. We can kinda just look at a map and if the problem is small enough we can come up with something that's, y'know, not a bad attempt.
And yet given all of that it actually is really hard! Thousands of person-years have been spent trying to find better solutions to it.
So what is the simplest possible solution that finds the shortest route? Just check every possible tour and see which one is shortest! Let's say we start with n cities. Then how many tours are there to check? We need to unpack the definition of the problem to conclude two things. First, that it doesn't matter where you start your solution: since any solution is a tour and there are no one-way roads you can pick any starting location on the tour and loop around and get the exact same distance. It also doesn't matter whether start by going "left" or "right" when you're traversing a solution, which means we're going to have to divide our final answer in half to account of the symmetry. Now we pick a starting location, it doesn't matter what, and we have n-1 next cities to choose from. After choosing that city we have n-2 cities to choose from for the next destination. We can repeat that process until we have only 1 city to choose from, which is the start.
How many possible routes does that give us? Remember that when we have a bunch of choices to make we multiply the possibilities together. So it's (n-1)*(n-2)*(n-3)...2*1. Well that's just the function (n-1)!. Now we divide in two because of symmetry and we get that the number of routes is (n-1)!/2.
So the simplest possible approach gives us an answer in something proportional to (n-1)! steps to check. If you don't remember how fast factorial grows it's helpful to note that
5! = 12010! = 3628800or a little over 3.6 million20! ~ 2.4 * 10^18so approximately 24 followed by 17 zeros
Okay so the naive solution isn't very feasible for any kind of large problem. That's obvious. But surely we can do a lot better, right?
Well that's where it gets interesting. The answer is sorta but not really.
This is an example of hard problem. NP-hard specifically! We're not going to explain everything about complexity classes but I want to at least make some of the basics clear.
P is a collection, a set, of problems in computer science that can be solved by a computer in polynomial time, that is that the size of the problem grows like n^m for some fixed m. Don't necessarily think of these as the problems you can solve fast but more like the problems that scale slowly enough that computers getting faster will actually buy you something.
The other class of problems we talk about a lot is NP. What does the N in NP stand for? When I first saw these concepts ages I go I thought "not, obviously". They're not polynomial. Which is sorta (probably) true! But actually N stands for "non-deterministic", so these are problems that can be solved in polynomial time "non-deterministically", which basically means that they can be solved in polynomial time if you have a magical computer that can actually try every possible choice at once.
Also, please note, that sometimes that "try every possibility at the same time" language is how people describe quantum computers. That's not a quantum computer. Quantum computers are weirder and cooler than that, but that's outside the scope of what we're talking about today. I'm just hoping to sound a little mysterious so you'll want to learn more about quantum computers.
So when we're calling the taveling salesman NP-hard that doesn't just mean "it's hard like an NP problem" it means "it's at least as hard as any NP problem in that if you could solve the traveling salesman in polynomial time you will have proved you can solve all NP problems in polynomial time".
Alright so is the game over? Well, no, like even back in the 60s there were tricks that involved dynamic programming—which is where you are clever about breaking a problem down into sub-problems so that you can avoiding recalculating data—to get to something that grows like n^2*2^n which still isn't great but it's at least a lot better in terms of where you go from "okay we can compute this" to "nope, not in our lifetime". For example, if 20! is 24 followed by 17 zeros then 20*20*2^20 is a mere 42 followed by 7 zeros. That's a big difference. There are better solvers still today that use techniques like "integer programming", which I'll at the very least include on an assignment before the term is done so you can get a sense of how it work, and the largest exact solution I've been able to find—surprisingly—is still an old solution of a 85,900 location problem in 2006 that Bell Labs calculated for laser engraving when designing a chip. As far as I can tell newer research on exact solutions seems to have been in terms of new hardware architectures that expand the reach of what smaller traveling salesman problems can be done effectively immediately (see: https://www.eurekalert.org/news-releases/840425)
Now, this brings us to the last thing I wanted to talk about: heuristics. Sometimes, perfect isn't what you need, you just need good enough. I mean sure if you're Intel or NVidia or Qualcomm wanting to optimize some piece of silicon that you're going to make a trillion of maybe "good enough" won't be good enough. But if I want to make sure that my 3d printer that's printing out my design maybe five times maybe good enough isn't so bad.
For example, and I honestly love this result, let's do something that seems downright silly. We pick a starting point and then just go to the place closest by. Then we got to the place closest by that (that we haven't visited before). Then we just repeat this process until we're done. This is called the nearest neighbors heuristic. What's really cool is that all the way back in the 70s someone proved that the worst this could even do, for large problems, is a factor of 2x worse than the real shortest path. Again, if you're optimizing some big industrial process maybe that's not good enough, but if you just want your 3d printer to run kinda okay, if you want some drone delivery service to be not too far off the mark, then honestly knowing that it'll never be worse than a factor of 2 than the shortest route might be good enough. I've seen the claim, but not been able to verify, that when you experimentally look at the nearest neighbors heuristic vs. exact solutions it averages to something around 1.25 times worse, so 25% worse. If it's true, that's pretty cool.
We can see how this works with our previous example, in this case it gives us a length of 66
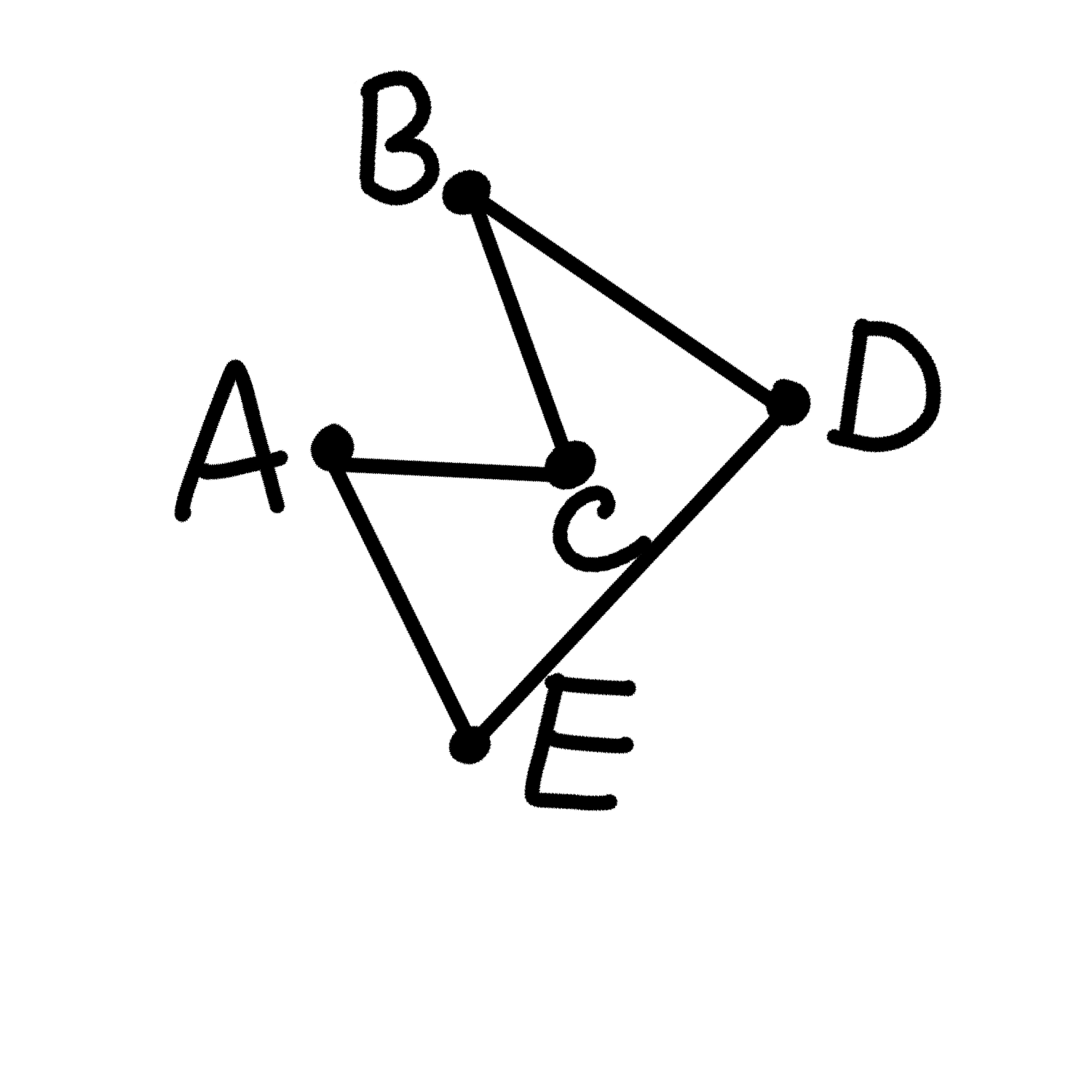
What's the complexity of this problem? Well, you're roughly making n moves and each time you make a move you make roughly n comparisons (n-1 at the beginning, 1 at the end, it averages out to be n/2), so this grows like n^2. Not bad!
Now the last thing to talk about is what is, essentially, still the state of the art in approximations (although in the past decade people have managed to very subtly improve on it by a small fraction of a percent!): Christofides's algorithm.
Talking about how it works is beyond the scope of this class but the basic idea is that you
- don't worry about building a tour, just build the tree that connects the whole map together that has the smallest total distance
- add back in edges between the closest end nodes
- eliminate the backtracking and redundancies
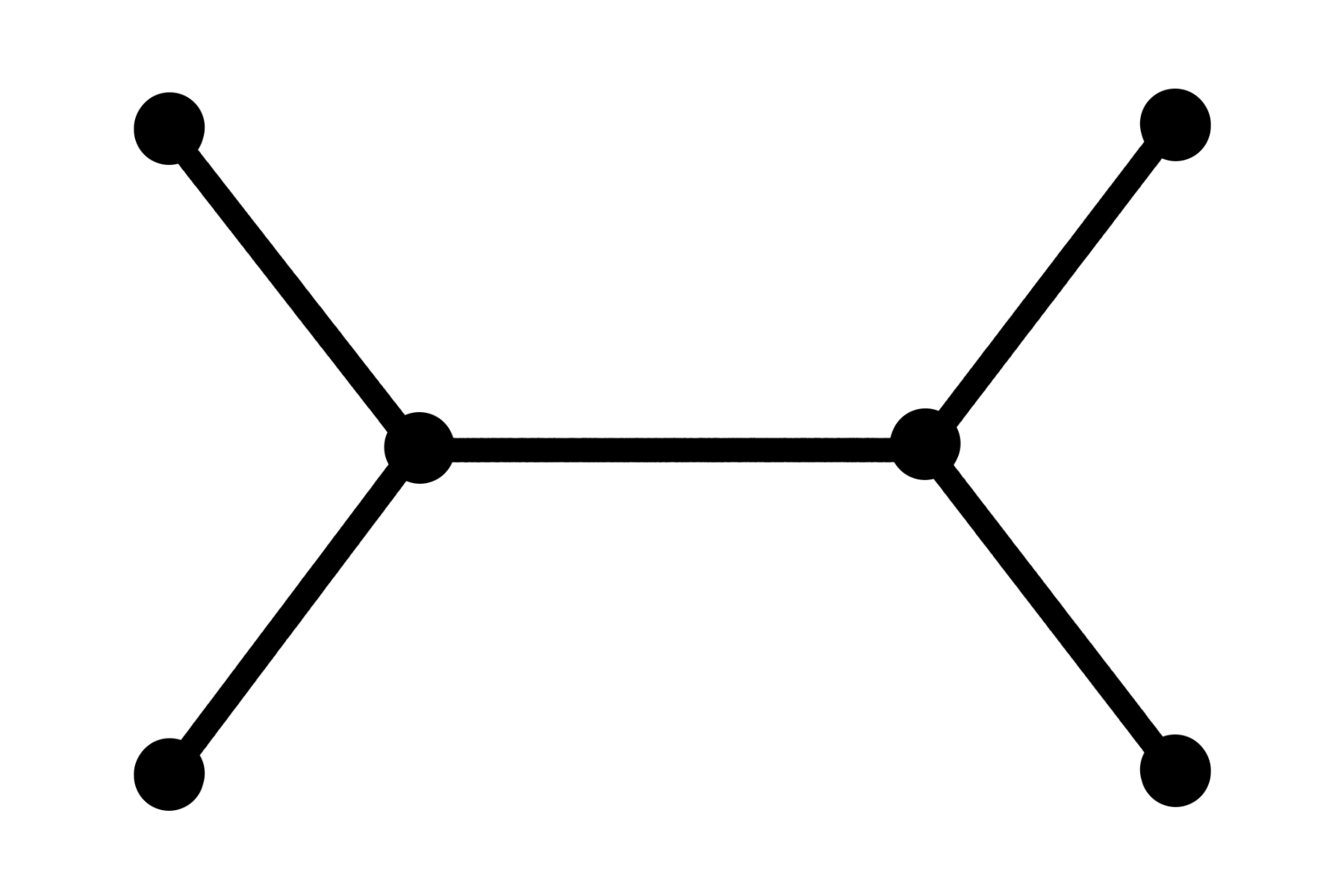
Here's an example inspired by one from William Cook's book In pursuit of a traveling salesman
A graph for an instance of the TSP

The graph connected together minimally
The graph connected together with closest end-points matched together
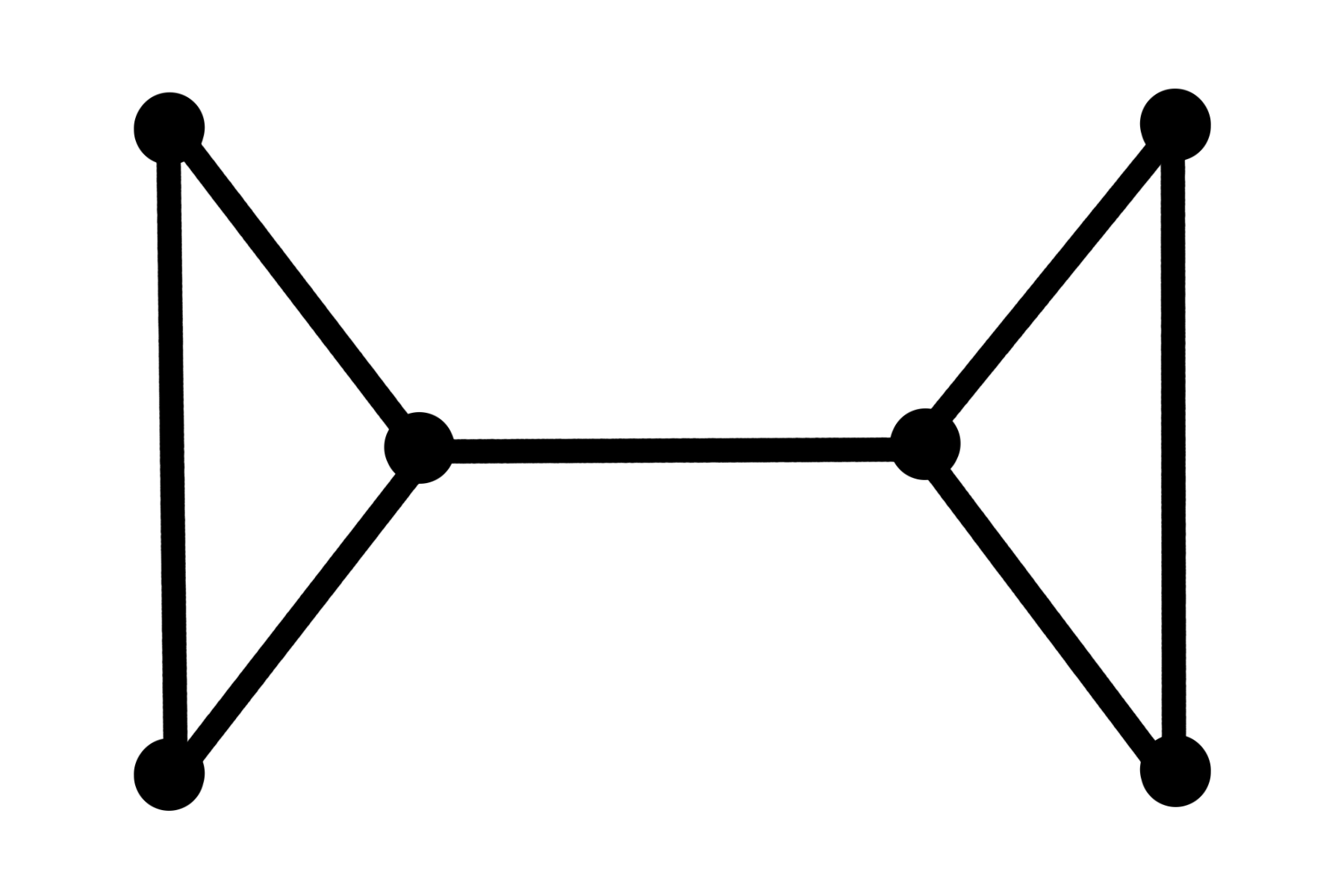
The graph with redundancies removed to turn it into a tour
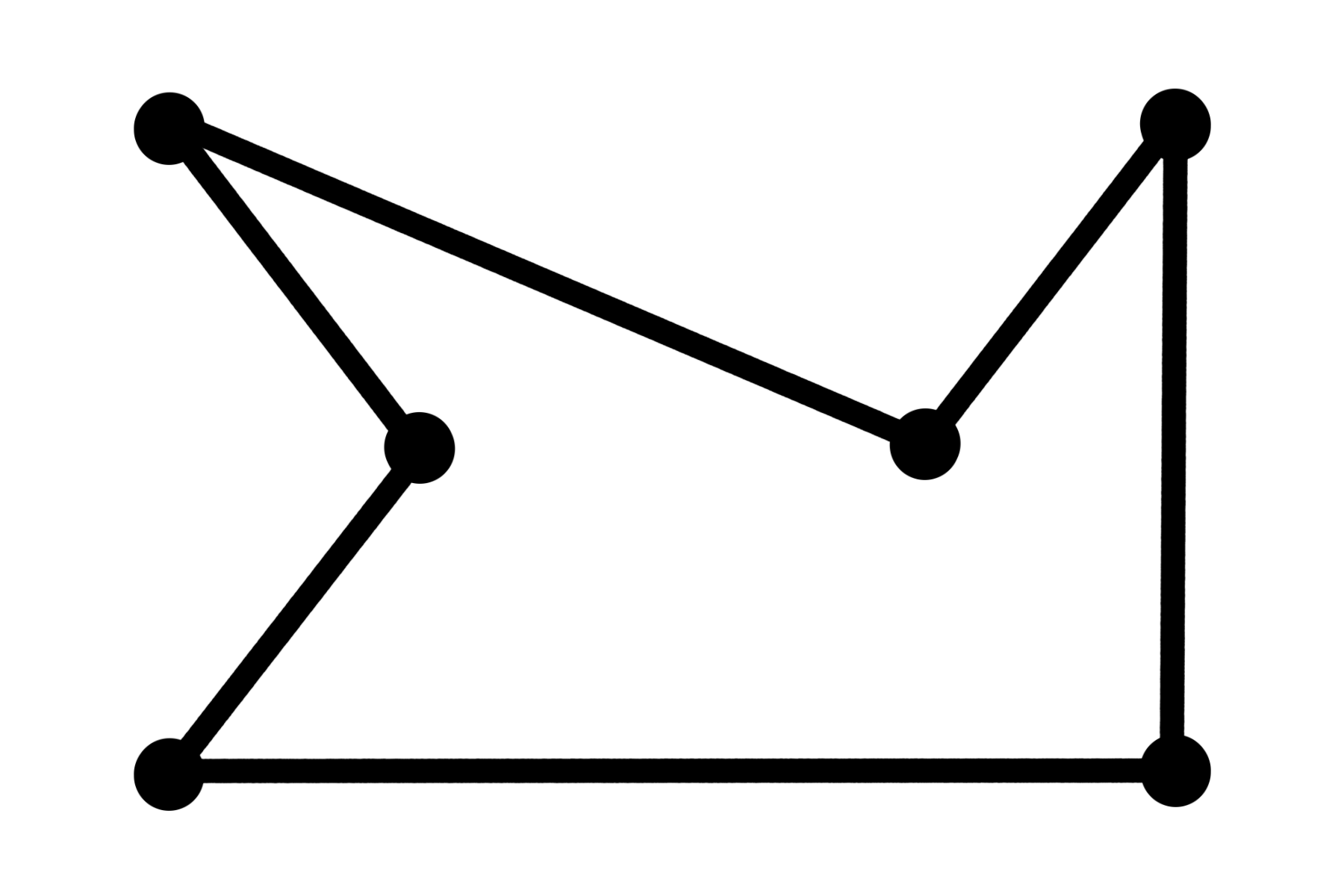
This runs a little worse, more like n^3, but it's at worst only 50% worse than the exact solution. That's honestly really cool.
So that's a whirlwind tour of the traveling salesman problem, probably one of the most studied and infamous problems in computer science.